Particle Motion

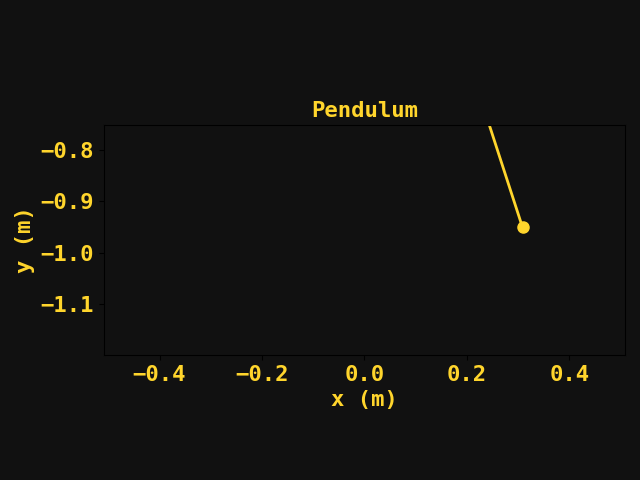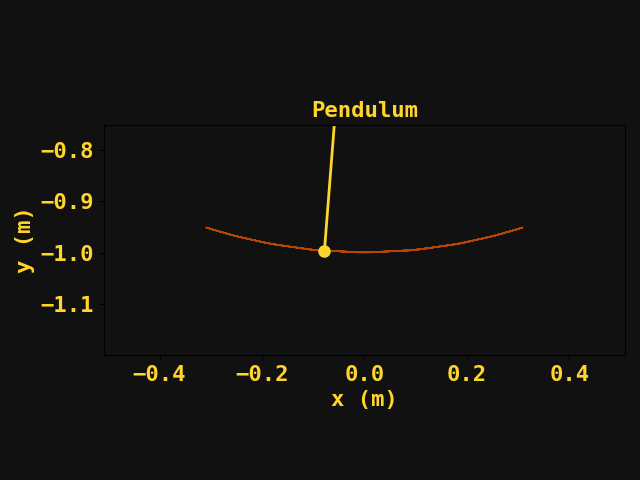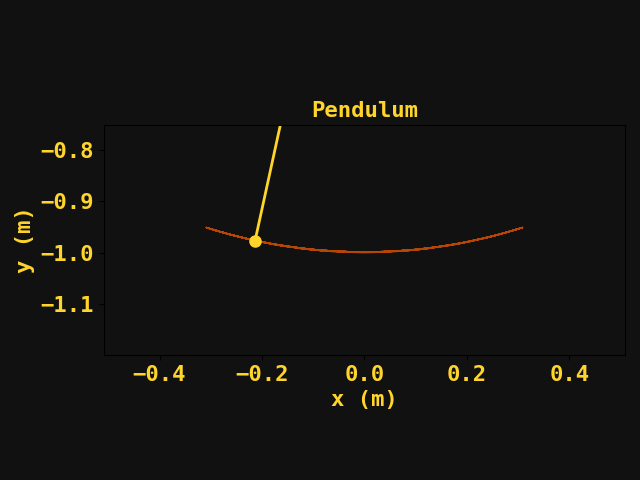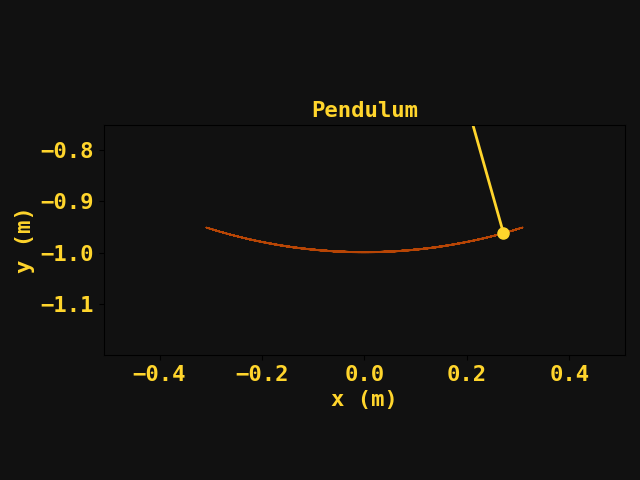
  When it came to physics, motion was just not my jam, in fact, it was my worst topic in the physics series. Yet, recently I've found myself delving into the world of computational physics. I never really had to use a computer to solve many physics problems until I got into semiconductor modeling. Even then, we worked with suites that handled a lot of the nuances of computation and so many things 'worked under the hood' so to speak. Ultimately, I wanted to learn how physics problems are solved using computers. So I found a textbook (link here?) and got to work. And as with any skill - I started with the most basic of problems: particle motion.

A Simple Pendulum

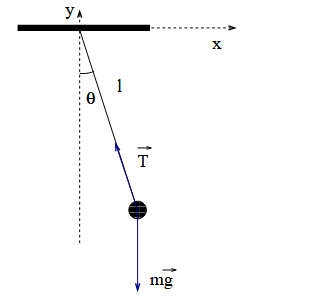
The equations of motion involving a simple pendulum system are well known and can be dervied using a free-body diagram and some trigonometry. If you haven't done something like this in a while I'd say it's good practice but I'll spare you the derivation since there are plenty of walkthroughs of the problem available online. The equations of motion are as follows:

$$\theta = \theta_0 \cos(\omega (t - t_0)) \\ \frac{d\theta}{dt} = - \omega \theta_0 \sin(\omega(t-t0))\\ x(t) = l \sin(\theta)\\ y(t) = -l \cos(\theta)\\$$

Where \(\omega = \sqrt{\frac{g}{l}}\) and we note that this solution is only applicable for small angles of \( \theta\ \lt \lt 1 \). Assuming we are given \( \theta_0\) and \( l \) we can now plot the position of the bob as a function of time.

Time

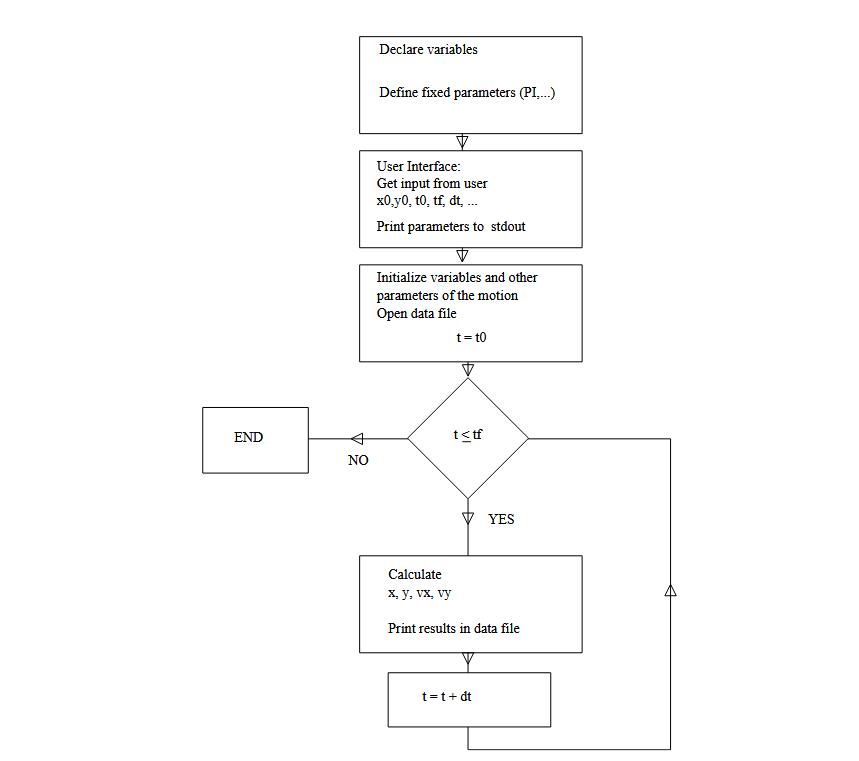
The logic of the program will involve starting at an initial time value \(t_0\) and then continually evaluating \(x(t) \) and \(y(t) \). After evaluation, we'll step forward in time by a step of \(dt \) and repeat the process until we've reached the final time, \(t_f\).

Code

I ended up using python to implement the program and used matplotlib's animation module to render the gif.

Overall this was a nice little introduction to the framework of working with equations of motion. Below I'll post a few more animations I made for different systems. What comes next is an investigation into the convergence of the solution for different systems.